设计任务:矩阵A中的元素若满足:A[i,j]是第i行中值最小的元素,且又是第j列中值最大的元素,则称元素A[i,j]为该矩阵的一个马鞍点。求出m*n矩阵的所有马鞍点。
要求:使用二维数组、堆分配数组、三元组、十字链表完成上述操作并比较效率。
- 设计题目与设计任务(设计任务书)
用不同的存储结构实现寻找m*n的矩阵中的马鞍点的算法。
- 前言(绪论)(设计的目的、意义等)
鞍点(Saddle point)在微分方程中,沿着某一方向是稳定的,另一条方向是不稳定的奇点,叫做鞍点。在泛函中,既不是极大值点也不是极小值点的临界点,叫做鞍点。在矩阵中,一个数在所在行中是最大值,在所在列中是最小值,则被称为鞍点。在物理上要广泛一些,指在一个方向是极大值,另一个方向是极小值的点。所以,寻找马鞍点的算法研究是十分有必要的。
- 设计主体(各部分设计内容、分析、结论等)
3.1需求分析
该程序主要功能是在一个m*n的矩阵中寻找马鞍点,如果马鞍点存在,则输入该马鞍点的位置信息以及该点的值;如果马鞍点不存在,则输出“没有马鞍点”的提示信息。
程序流程图:

输入形式:
首先输入两个数字,代表矩阵的行数m和列数n。
然后输入m行n列的矩阵。
输出形式:如果马鞍点存在,则输出马鞍点的位置和值,否则输出“没有马鞍点”。
测试样例1:
输入:
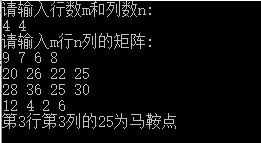
4 4
9 7 6 8
20 26 22 25
28 36 25 30
12 4 2 6
输出:
第3行第3列的25为马鞍点
测试样例2:
输入:
5 5
9 5 3 4 8
8 4 5 1 7
5 4 7 2 3
5 8 6 2 1
4 5 7 6 9
输出:
没有马鞍点
3.2系统实现
通过O(n2)时间复杂度的对数组的遍历,寻找出数组中每一行的最小的数字,并存储在数组minn中,寻找出数组中每一列的最大的数字,并存储在数组maxx中,如果minn和maxx数组中存在相同的数则说明该数为该矩阵的马鞍点。
3.3用户手册
此时输入两个数字,代表行和列

此时输入我们的2行2列的矩阵


3.4测试
测试样例1:
测试样例2:

3.5效率比较
下面四种方法的时间复杂度均为O(n2)。
二维数组法:定义方便,但不能灵活的控制内存空间。
堆分配数组法:能灵活的控制内存空间,能自由的控制数组的生存时间。
三元组法:在该程序中代码较为复杂,且花费了更多的空间。
十字链表法:在稀疏矩阵的时候能够省下较多的存储空间,但代码较为复杂。
二维数组法代码:
#include<iostream>
#include<cstring>
using namespace std;
int main()
{
int m ,n;
bool flag = false;
cout<<"请输入行数m和列数n:"<<endl;
cin>>m>>n;
cout<<"请输入m行n列的矩阵:"<<endl;
flag = false;
int minn[n+1];
int maxx[m+1];
memset(minn,0,sizeof(minn));//把数组置为0
memset(maxx,0,sizeof(maxx));//把数组置为0
int a[m+1][n+1];
for(int i = 0; i<m; i++)
{
for(int j = 0; j<n; j++)
{
cin>>a[i][j];
}
}
for(int i=0; i<m; i++) //求出每行最小数,存在minn数组中
{
minn[i]=a[i][0];
for(int j=1; j<n; j++)
if(minn[i]>a[i][j])
minn[i]=a[i][j];
}
for(int j=0; j<n; j++) //求出每列最大数,存在maxx数组中
{
maxx[j]=a[0][j];
for(int i=1; i<m; i++)
if(maxx[j]<a[i][j])
maxx[j]=a[i][j];
}
for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
if(minn[i]==maxx[j])//找到马鞍点
{
cout<<"第"<<i+1<<"行第"<<j+1<<"列的"<<a[i][j]<<"为马鞍点"<<endl;//i+1 j+1原因:第几行第几列从1开始,而数组从0开始
flag = true;
}
}
}
if(flag == false)
{
cout<<"没有马鞍点"<<endl;
}
}
堆分配数组法代码:
#include<iostream>
#include<cstring>
#include<stdlib.h>
using namespace std;
int main()
{
int m ,n;
bool flag = false;
cout<<"请输入行数m和列数n:"<<endl;
cin>>m>>n;
cout<<"请输入m行n列的矩阵:"<<endl;
flag = false;
int *minn = (int*)malloc(n*sizeof(int));
int *maxx = (int*)malloc(m*sizeof(int));
memset(minn,0,sizeof(minn));//把数组置为0
memset(maxx,0,sizeof(maxx));//把数组置为0
int **a=(int**)malloc(sizeof(int*)*m);
for(int i=0; i<m; i++)
{
a[i]=(int*)malloc(sizeof(int)*n);
}
for(int i = 0; i<m; i++)
{
for(int j = 0; j<n; j++)
{
cin>>a[i][j];
}
}
for(int i=0; i<m; i++) //求出每行最小数,存在minn数组中
{
minn[i]=a[i][0];
for(int j=1; j<n; j++)
if(minn[i]>a[i][j])
minn[i]=a[i][j];
}
for(int j=0; j<n; j++) //求出每列最大数,存在maxx数组中
{
maxx[j]=a[0][j];
for(int i=1; i<m; i++)
if(maxx[j]<a[i][j])
maxx[j]=a[i][j];
}
for(int i=0; i<m; i++)
{
for(int j=0; j<n; j++)
{
if(minn[i]==maxx[j])//找到马鞍点
{
cout<<"第"<<i+1<<"行第"<<j+1<<"列的"<<a[i][j]<<"为马鞍点"<<endl;//i+1 j+1原因:第几行第几列从1开始,而数组从0开始
flag = true;
}
}
}
if(flag == false)
{
cout<<"没有马鞍点"<<endl;
}
free(minn);
free(maxx);
free(a);
}
三元组法代码:
#include<iostream>
#include<cstring>
#include<stdlib.h>
using namespace std;
typedef struct
{
int i,j,e;
} Triple; //数据类型 三元组
typedef struct
{
Triple *base; //矩阵基址
int MatrixSize; //当前的矩阵大小
int mu,nu; //当前长度
} Matrix; //矩阵抽象数据类型
int main()
{
while(1)
{
bool flag = false;
int m,n,p=0;
int value;
Matrix a;
cout<<"请输入行数m和列数n:"<<endl;
cin>>a.mu>>a.nu;
a.base=(Triple *)malloc(a.mu*a.nu*sizeof(Triple));
cout<<"请输入m行n列的矩阵:"<<endl;
flag = false;
int minn[a.mu];
int maxx[a.nu];
memset(minn,0,sizeof(minn));//把数组置为0
memset(maxx,0,sizeof(maxx));//把数组置为0
for(int i = 0; i<a.mu; i++)
{
for(int j = 0; j<a.nu; j++)
{
cin>>a.base[p].e;
a.base[p].i = i;
a.base[p].j = j;
p++;
}
}
p = 0;
int row,col;
int q=0,order=0;
for(row=1; row<=a.mu; row++)
{
p=(row-1)*a.nu;//行首元素的下标
minn[row]=a.base[p].e; //令每行的第一个元素为最小值
for(col=2; col<=a.nu; col++) //从每行的第二个元素开始遍历
{
p++; //同一行元素存储位置连续,下标下移
if(minn[row]>a.base[p].e)
minn[row]=a.base[p].e;
}
}
for(col=1; col<=a.nu; col++)
{
maxx[col]=a.base[col-1].e;//令每列的第一个元素为最大值
for(row=2; row<=a.mu; row++) //从每列的第二个元素开始遍历
{
q=(row-1)*a.nu+col-1;//col列的第row个元素的下标,完成同一列元素的依次遍历
if(maxx[col]<a.base[q].e)
maxx[col]=a.base[q].e;
}
}
for(p=1; p<=a.mu; p++)
{
for(q=1; q<=a.nu; q++)
{
if(minn[p]==maxx[q])
{
cout<<"第"<<p<<"行第"<<q<<"列的"<<minn[p]<<"为马鞍点"<<endl;
flag = true;
}
}
}
if(flag == false)
{
cout<<"没有马鞍点"<<endl;
}
}
}
十字链表法代码:
#include<stdio.h>
#include<stdlib.h>
#include<iostream>
#include<limits.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define INFEASIBLE -1
using namespace std;
typedef int ElemType;
typedef struct OLNode
{
int i,j;
ElemType e;
struct OLNode *right, *down;
} OLNode, *OLink;
typedef struct
{
OLink *rhead, *chead;
int mu,nu,tu;
} CrossList;
int CreateSMatrix_OL(CrossList *M)
{
if(M) free(M);
int m,n,t=0;
printf("请输入行数m和列数n:\n");
scanf("%d%d",&m,&n);
printf("请输入m行n列的矩阵:\n");
M->mu=m;
M->nu=n;
if(!(M->rhead=(OLink *)malloc((m+1)*sizeof(OLink)))) return ERROR;
if(!(M->chead=(OLink *)malloc((n+1)*sizeof(OLink)))) return ERROR;
int a,b;
for (a=1; a<=m; a++) M->rhead[a]=NULL;
for (b=1; b<=n; b++) M->chead[b]=NULL;
int i,j,e;
for(i=1; i<=m; i++)
{
for(j=1; j<=n; j++)
{
scanf("%d",&e);
if(e!=0)
{
t++;
OLNode *p,*q;
if(!(p=(OLNode *)malloc(sizeof(OLNode)))) return ERROR;
p->i=i;
p->j=j;
p->e=e;
p->down=NULL;
p->right=NULL;
if(M->rhead[i]==NULL||M->rhead[i]->j>j)
{
p->right=M->rhead[i];
M->rhead[i]=p;
}
else
{
for(q=M->rhead[i]; (q->right)&&q->right->j<j; q=q->right);
p->right=q->right;
q->right=p;
}
if(M->chead[j]==NULL||M->chead[j]->i>i)
{
p->down=M->chead[j];
M->chead[j]=p;
}
else
{
for(q=M->chead[j]; (q->down)&&q->down->i<i; q=q->down);
p->down=q->down;
q->down=p;
}
}
}
}
M->tu=t;
return OK;
}
void print(CrossList M)
{
int p,q;
OLNode *pTemp;
for(p=1; p<=M.mu; p++)
{
pTemp=M.rhead[p];
for(q=1; q<=M.nu; q++)
{
if(pTemp!=NULL&&pTemp->j==q)
{
printf("%d ",pTemp->e);
pTemp=pTemp->right;
}
else
printf("0 ");
}
printf("\n");
}
}
void findPoint(CrossList M)
{
bool flag = false;
int p,q;
int minn[M.mu];
int maxx[M.nu];
maxx[0] = INT_MIN;
minn[0] = INT_MAX;
OLNode *pTemp;
for(p=1; p<=M.mu; p++)
{
pTemp=M.rhead[p];
minn[p-1] = INT_MAX;
for(q=1; q<=M.nu; q++)
{
if(pTemp!=NULL&&pTemp->j==q)
{
if(pTemp->e < minn[p-1])
{
minn[p-1] = pTemp->e;
}
pTemp=pTemp->right;
}
else
{
if(minn[p-1]>0){
minn[p-1] = 0;
}
}
}
}
for(p=1; p<=M.nu; p++)
{
pTemp=M.chead[p];
maxx[p-1] = INT_MIN;
for(q=1; q<=M.mu; q++)
{
if(pTemp!=NULL&&pTemp->i==q)
{
if(pTemp->e > maxx[p-1])
{
maxx[p-1] = pTemp->e;
}
pTemp=pTemp->down;
}
else
{
if(maxx[p-1]<0){
maxx[p-1] = 0;
}
}
}
}
for(p=1; p<=M.nu; p++){
cout<<maxx[p-1]<<" ";
}
for(int i=0; i<M.mu; i++)
{
for(int j=0; j<M.nu; j++)
{
if(minn[i]==maxx[j])//找到马鞍点
{
cout<<"第"<<i+1<<"行第"<<j+1<<"列的"<<minn[i]<<"为马鞍点"<<endl;//i+1 j+1原因:第几行第几列从1开始,而数组从0开始
flag = true;
}
}
}
if(flag == false)
{
cout<<"没有马鞍点"<<endl;
}
}
int main()
{
while(1){
CrossList M;
CreateSMatrix_OL(&M);
findPoint(M);
return 0;
}
}